Покорение RSA на C#. Часть 2

В прошлой статье про RSA я написал, как реализовал на C# базовый математический алгоритм RSA. Но гладко было на бумаге, да забыли про овраги.

Я настроил программу на реальные данные — запустил расшифровку 128-байтного сообщения 128-байтным (1024-битным) ключом:

string sKeyPow = "10001"; //около 65.000 в десятичной системе
string sKeyMod = "00AB25073527C39B1E934213870AB19D9CC4AF7C037F44F92462F7A896F6A22AF798741F39CD3F133BB96B13C11C8E105F231CBCBBDBA1F9BD876F07FF93151FB9E971331FB604C6A17998BDF772032DAA1DD17662D4926E8F502A22FBCE377A45595EAE7446727E777FDC4781E56E84548A9390855168DBA68E07E33D3B9BF097"; //258 длина, 128 байт
string sCoded = "681FA51781F3AA4727C72374C6FE68A1C0BD3081DB1026C715CC791CA7F1CCF076143A9D15813641B2C533AE0064934B510ED42D430196A16EC9EE65743EA3E03CF674DABAF05FA647898344DB65D325A130B511E68A33E0995273D36049CBBF206E3BEE021360AACF03C12347D600DD70E34389A007704771525E11548E9DDB"; //256
string s = myRSA.RSA_Decode(sCoded, sKeyPow, sKeyMod);

К моему удивлению, IDE завис на вычислении 65-тысячной степени 1024-битного числа. На картинке подсчет идёт уже 9 минут и останавливаться не планирует:

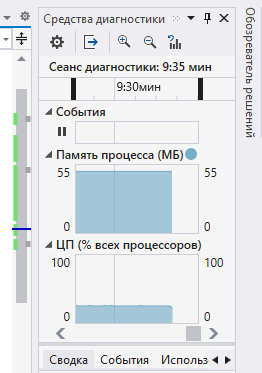
Тогда я понял, что пример, который я смотрел, работает только на ключе небольшого размера и решил попробовать все же разобраться, как работать с типовой криптографией RSA из NET.

Я возился примерно час, разбираясь в нюансах объектной модели и изучая примеры в интернете. В итоге получилось что-то похожее на рабочую модель:

static public string RSA_Decode_RSA(string sInput, string sKeyExp, string sKeyMod)
{
 
    RSACryptoServiceProvider RSA = new RSACryptoServiceProvider();
    //RSAParameters privateKey = RSA.ExportParameters(true);
    //RSAParameters publicKey = RSA.ExportParameters(false);
    RSAParameters RSAPrm = new RSAParameters();
    RSAPrm.Exponent = HexStrToByteArray(sKeyExp);
    RSAPrm.Modulus = HexStrToByteArray(sKeyMod);
    RSA.ImportParameters(RSAPrm);
    string publicxml = RSA.ToXmlString(false); //https://stackoverflow.com/questions/27383623/c-sharp-get-public-key-from-modulus-and-exponent
    byte[] result = RSA.Decrypt(HexStrToByteArray(sInput), false);
 
 
    return "";
}
 

Увы, функция Decrypt выдавала ошибку «Ключ не найден». Я почитал еще и понял, что криптография от Microsoft может не работать для классического RSA. По крайней мере, она не умеет шифровать открытым ключом, например и в примерах писали это шифрование своими силами.

Я решил вернуться к своей реализации RSA, но немного расстроился, т.к. не было никаких идей, как ускорить расчет. Я нашел способ ускорения возведения в степень, но это не помогло:

static BigInteger QuickPower(BigInteger x, int n)
{
    BigInteger result = 1L;
    while (n > 0)
    {
        if ((n & 1) == 0)
        {
            x *= x;
            n >>= 1;
        }
        else
        {
            result *= x;
            --n;
        }
    }
 
    return result;
}
 

Где-то я прочитал, что т.к. нужна не сама степень, а остаток от деления, существую алгоритмы, которые вычисляют эту функцию быстрее.

Но было уже поздно, поэтому я нашел в себе силы только сформулировать вопрос на sql.ru:

Каково же было мое удивление, когда утром в моей ветке мне предложили удивительно простое решение:

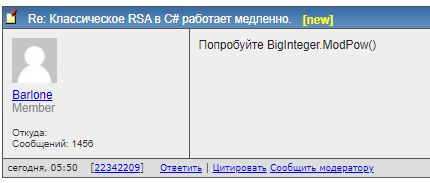
Дрожащими от радостного возбуждения руками я поправил свой код и расчет пролетел мгновенно:

static public string RSA_Decode(string sInput, string sKeyExp, string sKeyMod)
{
    //All strings are Hex
 
    string result = "";
 
 
    BigInteger biInput = BigInteger.Parse("0" + sInput, System.Globalization.NumberStyles.AllowHexSpecifier);
    BigInteger biKeyExp = BigInteger.Parse("0" + sKeyExp, System.Globalization.NumberStyles.AllowHexSpecifier);
    BigInteger biKeyMod = BigInteger.Parse("0" + sKeyMod, System.Globalization.NumberStyles.AllowHexSpecifier);
 
    //About hex: https://stackoverflow.com/questions/30119174/converting-a-hex-string-to-its-biginteger-equivalent-negates-the-value
    //BigInteger bi = BigInteger.Pow(biInput, (int) biKeyExp);
    //BigInteger bi = QuickPower(biInput, (int) biKeyExp);
 
    //bi = bi % biKeyMod;
    BigInteger bi = BigInteger.ModPow(biInput, biKeyExp, biKeyMod);
 
    result = bi.ToString("X").ToUpper();
 
    return result;
}
 

Я поблагодарил советчика. Дальнейшее было уже делом техники!

Все-таки я остановился на классическом алгоритме RSA и не полез в дебри объектной модели Microsoft для ее реализации RSA. Понятно, что старое RSA возможно, несколько уязвимо, поэтому Microsoft его не поддерживает, но в рабоче-крестьянских целях для узких ниш оно вполне даже ничего.